Định lý Menelaus và Định lý Ceva

Định lý Menelaus

Bách khoa toàn thư mở Wikipedia

Buớc tưới chuyển hướngBước tới tìm kiếm

Định lý Menelaus

Định lý Menelaus là một định lý cơ bản trong hình học tam giác, được phát biểu như sau: Cho tam giác ABC. Các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi

Chứng minh

*Phần thuận: Giả sử D, E, F thẳng hàng với nhau. Vẽ đường thẳng qua C và song song với AB cắt đường thẳng DE tại G.
Vì CG//AB (c.dựng) nên theo định lý Ta-lét, ta có:
 (1) và  (2)
Nhân (1) và (2) và vế theo vế

Từ đó suy ra

*Phần đảo: Giả sử . Khi đó gọi F' là giao của đường thẳng ED với đường thẳng AB.
Theo chứng minh ở trên, ta có 
Kết hợp giả thuyết suy ra 
Hay 
Nên F'A = FA và F'B = FB
Do đó F' trùng với F.
Vậy định lý đã được chứng minh.

Định lý Ceva

Bách khoa toàn thư mở Wikipedia

Buớc tưới chuyển hướngBước tới tìm kiếm

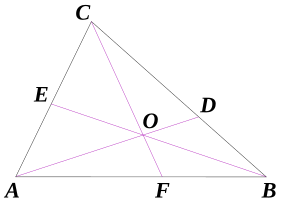
Định lý Ceva là một định lý phổ biến trong hình học cơ bản.Cho một tam giác ABC, các điểm D, E, và F lần lượt nằm trên các đường thẳng BC, CA, và AB. Định lý phát biểu rằng các đường thẳng AD, BE và CF là những đường thẳng đồng qui khi và chỉ khi:

${\displaystyle {\frac {\overline {FA}}{\overline {FB}}}\cdot {\frac {\overline {DB}}{\overline {DC}}}\cdot {\frac {\overline {EC}}{\overline {EA}}}=-1}$

Ngoài ra, định lý Ceva còn được phát biểu một cách tương đương trong lượng giác rằng: AD,BE,CF đồng qui khi và chỉ khi

${\displaystyle {\frac {\sin \angle BAD}{\sin \angle CAD}}\times {\frac {\sin \angle ACF}{\sin \angle BCF}}\times {\frac {\sin \angle CBE}{\sin \angle ABE}}=1}$.

Định lý Ceva

Một đường thẳng đi qua đỉnh của tam giác gọi là đường thẳng Cevianứng với đỉnh đó.Một trong hình vẽ tam giác ${\displaystyle DEF}$ là một tam giác Cevian của tam giác ABC.

Chứng minh định lý

Giả sử ta có: ${\displaystyle AD}$, ${\displaystyle BE}$ và ${\displaystyle CF}$ đồng qui tại một điểm ${\displaystyle O}$ nào đó (trong hay ngoài tam giác). Do ${\displaystyle \triangle BOD}$ và ${\displaystyle \triangle COD}$ có chung chiều cao (độ dài của đường cao), ta có: ${\displaystyle {\frac {|\triangle BOD|}{|\triangle COD|}}={\frac {BD}{DC}}.}$ Tương tự, ${\displaystyle {\frac {|\triangle BAD|}{|\triangle CAD|}}={\frac {BD}{DC}}.}$

Ta suy ra ${\displaystyle {\frac {BD}{DC}}={\frac {|\triangle BAD|-|\triangle BOD|}{|\triangle CAD|-|\triangle COD|}}={\frac {|\triangle ABO|}{|\triangle CAO|}}.}$ (1) Tương tự,${\displaystyle {\frac {CE}{EA}}={\frac {|\triangle BCO|}{|\triangle ABO|}},}$ (2) và${\displaystyle {\frac {AF}{FB}}={\frac {|\triangle CAO|}{|\triangle BCO|}}.}$ (3)

(1) x (2) x (3) cho ta:${\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1,}$(điều phải chứng minh).

Ngược lại, giả sử rằng ta đã có những điểm ${\displaystyle D}$, ${\displaystyle E}$ và ${\displaystyle F}$ thỏa mãn đẳng thức. Gọi giao điểm của ${\displaystyle AD}$ và ${\displaystyle BE}$ là ${\displaystyle O}$, và gọi giao điểm của ${\displaystyle CO}$ và ${\displaystyle AB}$ là ${\displaystyle F'}$. Theo chứng minh trên, ${\displaystyle {\frac {AF'}{F'B}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1.}$

Kết hợp với đẳng thức trên, ta nhận được: ${\displaystyle {\frac {AF'}{F'B}}={\frac {AF}{FB}}.}$

Thêm 1 vào mỗi vế và chú ý rằng ${\displaystyle AF'+F'B=AF+FB=AB}$, ta có ${\displaystyle {\frac {AB}{F'B}}={\frac {AB}{FB}}.}$

Do đó ${\displaystyle F'B=FB}$, vậy ${\displaystyle F}$ và ${\displaystyle F'}$ trùng nhau. Vì vậy ${\displaystyle AD}$, ${\displaystyle BE}$ và ${\displaystyle CF}$=${\displaystyle CF'}$ đồng qui tại ${\displaystyle O}$, và định lý đã được chứng minh (là đúng theo cả hai chiều).